Why Use Ten Frames and
Number Bonds?
A ten frame is a rectangular frame divided into two rows of five squares. Students can use counters or other manipulatives to fill in the squares. For example, different ways to make number 5 or all the ways to make number 10. They are especially useful in developing an understanding of addition and subtraction through 10 and place value of a two-digit number. Children internalize number patterns and learn to recognize a number, for example, 5 or 10, in different arrangements. In Singapore math, ten frames are often used in the early grades to build a strong foundation in number sense and place value.

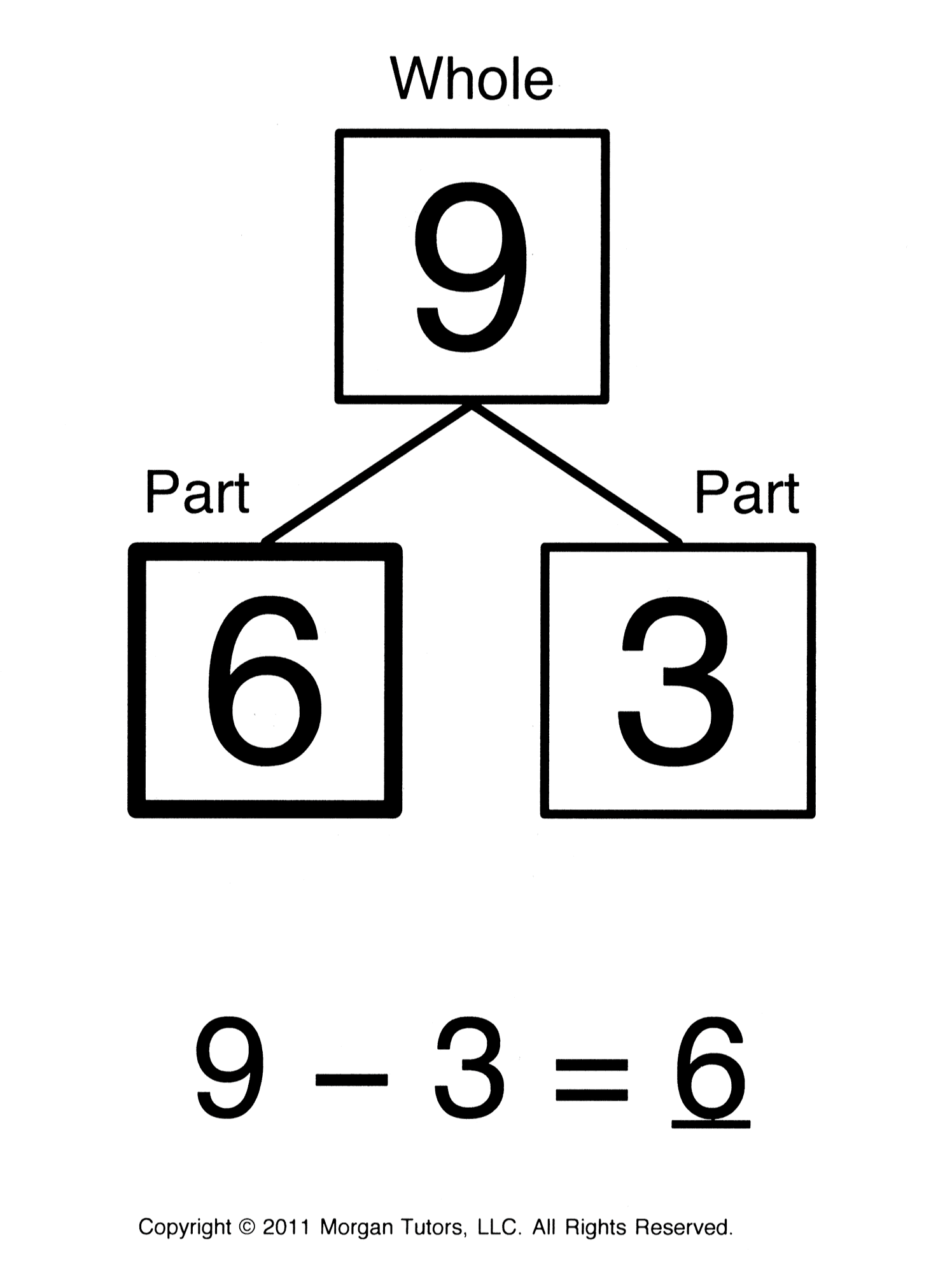
Special pictures called number bonds are used to look inside a number and break the whole into parts. For example, one way to make 9 is with parts of 3 and 6. The number 9 has many number bonds – 0 and 9, 2 and 7, 3 and 6, 4 and 5, and the turnaround bonds of 5 and 4, 6 and 3, 7 and 2 and 9 and 0.
Concrete and pictorial stages can be overlapped by using counters such as linking cubes (number trains) and placing them on top of the number bond picture. The number trains can be removed later as the child transfers the concrete experience to number bond pictures. The C-P-A process, which is used to connect manipulatives, pictures, and abstract math notation instills a deep understanding of mathematical ideas.
When children translate oral language stories or picture stories into number bond pictures, they can see the part-whole relationships and are able to recognize the story as an adding or subtracting story. English language or pictures can be turned into number bonds, and conversely, number bonds can be turned into math stories that later become word problems. Number bonds are also used for operations with bigger numbers when concrete materials or pictures of concrete objects are no longer practical.
Children develop good place value and number sense by using different number bond building and break apart strategies, first with numbers through 10 and 20 (math facts) and progressing to addition and subtraction with numbers through 100 and 1000. Using number bond strategies for mental computation strengthens students’ number sense and working memory by increasing their capacity to hold information in their heads. Number bonds continue to be used as a visual in more complex procedures such as long multiplication and long division as well as for mental math strategies in computing larger numbers without the need for column addition and subtraction procedures.
Number Bonds are also used in teaching operations involving composing or decomposing fractions and decimals. They’re an instrumental tool in mastering place value and understanding our base 10 number system. Because the Singapore approach uses number bonds early on and so consistently throughout the curriculum to break apart numbers, move numbers around, and put numbers back together, students are better prepared for Algebra which involves the manipulation of abstract symbols (variables, coefficients, term, etc.).